La folométrie, une invention de Cervione!

Définition:

Si 2 nombres qui sont multipliés ont le même résultat que ces 2 même additionnés, alors ils sont folométriques.

Nous allons chercher des nombres folométriques, et pour cela nous allons résoudre l’équation    x²=2x

x²–2x = 0 x(x–2) = 0 x=0   ou   x–2=0 x=0   ou   x=2

méthode: "on se ramène à zéro et on factorise" car si un produit est nul, alors au moins un de ses facteurs est nul.

Peut-on trouver d'autres nombres vérifiant le même genre de définition. Pour cela nous allons préciser cette première définition.

Définition:

Si n nombres qui sont multipliés ont le même résultat que ces n même additionnés, alors ils sont folométriques de degré n. c'est-à-dire axax...xa = a+a+...+a              an = nxa

C'est-à-dire que si additionner et multiplier parallèlement un nombre a par son degré n donne le même résultat, alors ce nombre a est folométrique de degré n.

D'après la définition précédente, 2 et 0 sont les seuls nombres folométrique de degré 2.

---

Cherchons alors les nombres folométriques de degré 3. Pour cela on résout l’équation

axaxa = a+a+a a3 = 3a a3–3a = 0 a(a2–3) = 0 a(a2–√32) = 0 a(a–√3)(a+√3) = 0 a=0   ou   a–√3=0   ou   a+√3=0 a=0   ou   a=√3   ou   a=-√3

méthode: "on se ramène à zéro et on factorise" car       a2–b2 = (a–b)(a+b) car si un produit est nul, alors au moins un de ses facteurs est nul.

Les nombres folométriques de degrés 3 sont donc -√3, 0 et √3.

---

Cherchons maintenant les nombres folométriques de degré 4.

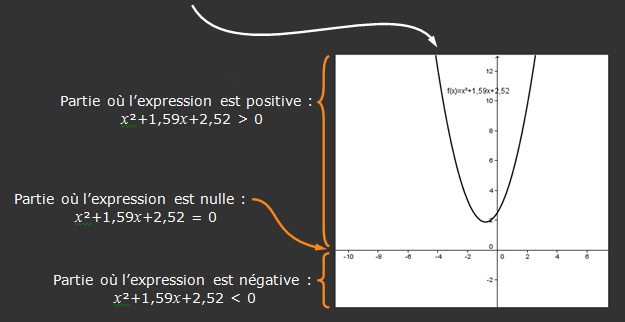
axaxaxa = a+a+a+a a4 = 4a a4–4a = 0 a(a3–4) = 0 a(a3–1,593) =0 a(a–1,59)(a2+1,59a+2,52) =0 a=0   ou   a–1,59=0   ou   a²+1,59a+2,52=0 a=0 ou a=1,59 ou    "impossible"	méthode: "on se ramène à zéro et on factorise" en posant 3√4=1,59... car       a3–b3 = (a–b)(a2+ab+b2) car si un produit est nul, alors au moins un de ses facteurs est nul.

On a tracé la courbe représentant l'expression x²+1,59x+2,52 après avoir calculé quelques valeurs (voir tableau ci-dessous).

x	-3	-2	-1	0	1	2
y=x²+1,59x+2,52	6,75	3,34	1,93	2,52	5,11	9,7

On constate que la courbe est dans la zone supérieure donc qu'elle ne passe pas par 0 (l'axe des abscisses). L'expression ne pourra donc jamais être nulle, on aura toujours      a²+1,59a+2,52≠0

Les nombres folométriques de degrés 4 sont donc 0 et ³√4=1.59...

---

Cherchons ensuite les nombres folométriques de degré 5.

axaxaxaxa = a+a+a+a+a a5 = 5a a5–5a = 0 a(a4–5) = 0 a((a2)2 –√52) = 0 a[a2–√5][a2+√5] = 0 a=0   ou  a2–√5=0  ou   a2+√5=0 a=0  ou   a2–2.24=0   ou   a2+2.24=0 a=0   ou   a2–√2,242=0   ou   impossible a=0   ou   (a–√2,24)(a+√2,24)=0 a=0  ou   a–√2,24=0  ou   a+√2,24=0 a=0   ou   a=√2,24   ou   a=-√2,24

méthode: "on se ramène à zéro et on factorise" car       a2–b2 = (a–b)(a+b) car si un produit est nul, alors au moins un de ses facteurs est nul. on pose √5=2,24... un carré n'est jamais négatif,    a2=-2.24 est impossible

Les nombres folométriques de degrés 5 sont -√√5, 0 et √√5

---

Quelques autres …

Pour les nombres folométriques de degré 0, on résout l'équation    a⁰ =0a     c'est-à-dire    1=0.
L'égalité étant fausse, il n’y a pas de nombre folométrique de degré 0.

Pour les nombres folométriques de degré 1, on résout l'équation    a¹ =1a     c'est-à-dire    a=a.
L'égalité étant toujours vraie, tous les nombres sont folométriques de degré 1.

Pour les nombres folométriques de degré -1, on résout l'équation    a^-1 =-1a 
    c'est-à-dire    1=-a²       -1=a².
L'égalité étant impossible puisqu'un carré n'est jamais négatif, il n'y a pas de nombre folométrique de degré -1.