Dans l’Antiquité grecque, la musique faisait partie des mathématiques.
L’enseignement comportait deux grands domaines, celui des « sciences
» - si l’on peut dire - et celui des « lettres », comme
aujourd’hui. Plus précisément, les anciens distinguaient ce
qu’on a nommé dans la période romaine le quadriuium
(arithmétique, géométrie, musique et astronomie) d’une
part, le triuium (grammaire, dialectique et rhétorique) de l’autre.
Mais si l’on comprend aisément aujourd’hui pourquoi l’arithmétique,
la géométrie et même l’astronomie étaient rattachées
aux mathématiques, on ne voit guère pourquoi, à priori, la
musique était traitée de la même manière. C’est
ici que la connaissance des théories pythagoriciennes de la musique devient
nécessaire.
Les Grecs ont alors nommé ces intervalles entre deux notes, diapason pour des marteaux dont l’un pesait la moitié de l’autre, dipente pour les deux tiers de l’autre et enfin diatessaron pour le quart de l’autre. Aujourd’hui on appelle ses intervalles octave, quinte et quarte respectivement.
Les musiciens ont par la suite divisé l’octave en notes (7+1 pour chacune des octaves) et ont envisagé généralement 10 octaves, l'ensemble de ces octaves formant l'échelle musicale.
Les noms des notes, en France, sont : do ré mi fa sol la si (do). C'est Guido d'Arezzo [1000-1050] qui en est à l'origine, par son hymne "Ut queant laxis" où les premières notes de chaque vers étaient dans l'ordre naturel de la gamme :
(Do a remplacé UT au XVIIème siècle)
Calculons alors les rapports des masses qu’il faudrait donner aux divers marteaux pour reconstituer toutes les notes d’une octave. Choisissons pour le marteau du premier DO, l’unité.

Calculons maintenant les intervalles entre deux notes successives.
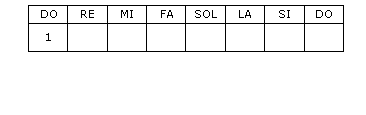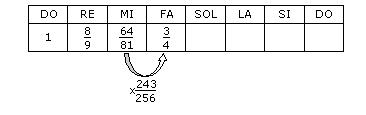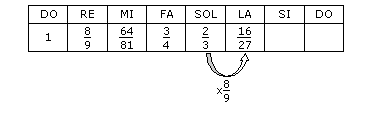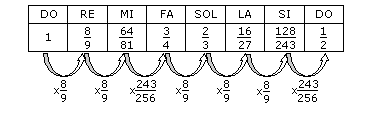
On peut constater que l’on obtient deux types d’intervalles différents : Ceux qui ont une longueur de 8/9 et ceux dont la longueur est de 243/256. Or si l’on double l’intervalle de longueur 243/256, on obtient un intervalle de longueur (243/256)² qui est proche de 8/9.
De cette simple remarque, on va nommer ces deux intervalles ton et demi-ton. Ainsi
On retrouve cette alternance de tons et de demi-tons sur les touches d’un piano où les touches noires représentent les demi-tons entre deux tons.
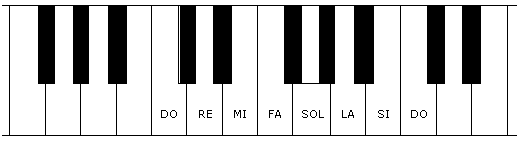
On constate que entre MI et FA ainsi qu’entre SI et DO, il n’y a pas de touches noires et que cela correspond à des intervalles de demi-tons.
Faut-il donc rétablir l'enseignement de la musique en cours de maths. Peut-être pas, car la musique est devenue une discipline à part entière, mais le lien entre ces deux matières devrait apparaître plus naturellement.
| On raconte que c’est en se promenant que Pythagore
découvrit les fondements des relations qui lient les mathématiques
et la musique. Jamblique, auteur du IVème siècle,
rapporte l’anecdote dans un des neufs livres qu’il écrivit
sur la secte pythagoricienne. « Par un coup divin du hasard, il
[Pythagore] passa devant l’atelier d’un forgeron et écouta
les marteaux battre le fer et produire à l’unisson une harmonie
variée d’échos, à l’exception d’une
seule combinaison. » Pythagore s’élança alors
dans l’atelier pour étudier l’harmonie des marteaux et
constata que ceux-ci, lorsqu’ils frappaient simultanément,
pouvaient produire un son harmonieux, mais qu’un marteau isolé
produisait toujours un son déplaisant. Il se rendit compte aussi,
que la hauteur (grave ou aigu) des sons dépendait non pas de la force
exercée par les hommes, mais seulement du poids des marteaux. Il entreprit alors d’examiner les marteaux et pu conclure que ceux qui, combinés, donnaient un son harmonieux, étaient liés par une relation mathématique simple : leurs masses étaient proportionnellement unies par des rapport simples ou étaient des fractions l’une de l’autre. Des marteaux pesant la moitié, les deux tiers ou le quart d’un marteau particulier, produisent ensemble des sons harmonieux (consonance), mais un marteau dont le poids n’a aucun rapport simple avec celui des autres, produit inévitablement, un son discordant (dissonance). |
 |
Les Grecs ont alors nommé ces intervalles entre deux notes, diapason pour des marteaux dont l’un pesait la moitié de l’autre, dipente pour les deux tiers de l’autre et enfin diatessaron pour le quart de l’autre. Aujourd’hui on appelle ses intervalles octave, quinte et quarte respectivement.
| Rentré chez lui, Pythagore associa les poids à des cordes également tendues de longueur proportionnelle aux poids. Pythagore tendit une corde sur une règle appelée canon où il avait marqué douze divisions. Alors, il commença par pincer la corde entière et sa moitié comportant six unités ; il trouva que le ton de la corde entière était symphone de celui de la moitié (6/12 = 1/2) selon l’octave… Puis il pinça de nouveau la corde entière et les trois quarts de celle-ci (9/12 = 3/4) et trouva que ces deux tons étaient symphones selon la quarte. Enfin, il pinça la corde entière et les deux tiers de celle-ci (8/12 = 2/3) et trouva cette fois-ci que les deux tons étaient symphones selon la quinte. |  |
Les musiciens ont par la suite divisé l’octave en notes (7+1 pour chacune des octaves) et ont envisagé généralement 10 octaves, l'ensemble de ces octaves formant l'échelle musicale.
Les noms des notes, en France, sont : do ré mi fa sol la si (do). C'est Guido d'Arezzo [1000-1050] qui en est à l'origine, par son hymne "Ut queant laxis" où les premières notes de chaque vers étaient dans l'ordre naturel de la gamme :
| UT queant laxis REsonare fibris MIra gestorum FAmuli tuorum SOLve polluti LAbii reatum Sancte Iohannes |
Calculons alors les rapports des masses qu’il faudrait donner aux divers marteaux pour reconstituer toutes les notes d’une octave. Choisissons pour le marteau du premier DO, l’unité.

Calculons maintenant les intervalles entre deux notes successives.

On peut constater que l’on obtient deux types d’intervalles différents : Ceux qui ont une longueur de 8/9 et ceux dont la longueur est de 243/256. Or si l’on double l’intervalle de longueur 243/256, on obtient un intervalle de longueur (243/256)² qui est proche de 8/9.
De cette simple remarque, on va nommer ces deux intervalles ton et demi-ton. Ainsi
| DO et RE | sont séparés par un | ton |
| RE et MI | sont séparés par un | ton |
| MI et FA | sont séparés par un | demi-ton |
| FA et SOL | sont séparés par un | ton |
| SOL et LA | sont séparés par un | ton |
| LA et SI | sont séparés par un | ton |
| SI et DO | sont séparés par un | demi-ton |
On retrouve cette alternance de tons et de demi-tons sur les touches d’un piano où les touches noires représentent les demi-tons entre deux tons.

On constate que entre MI et FA ainsi qu’entre SI et DO, il n’y a pas de touches noires et que cela correspond à des intervalles de demi-tons.
Faut-il donc rétablir l'enseignement de la musique en cours de maths. Peut-être pas, car la musique est devenue une discipline à part entière, mais le lien entre ces deux matières devrait apparaître plus naturellement.
 Le mot de la principale - U messaghju di a principale
Le mot de la principale - U messaghju di a principale




